Oleh: Michael A. Nielsen
(Sumber: Scientific American, Special Edition – The Edge of Physics, 31 Mei 2003, hal. 24-33)
Sebuah disiplin riset fundamental yang baru dan menggairahkan mengkombinasikan ilmu informasi dan mekanika quantum.
Selama beberapa dekade belakangan ini, para ilmuwan sudah tahu bahwa aturan sederhana bisa melahirkan perilaku amat kaya. Contoh yang bagus adalah catur. Bayangkan Anda seorang pemain catur berpengalaman yang diperkenalkan kepada seseorang yang mengklaim menguasai permainan ini. Lalu Anda bermain beberapa kali dan menyadari bahwa walaupun orang ini menguasai aturan catur, dia tak tahu cara bermain dengan baik. Dia membuat langkah-langkah absurd, mengorbankan ratu demi pion dan melepas benteng tanpa alasan sama sekali. Dia sungguh tak memahami catur: dia tak tahu prinsip tingkat tinggi dan heuristik yang dikenal oleh setiap pemain berpengetahuan. Prinsip-prinsip ini merupakan karakteristik catur yang kolektif atau darurat, fitur yang tidak muncul dari aturan tapi timbul dari interaksi antara bidak-bidak di papan catur.
Pemahaman mutakhir ilmuwan tentang mekanika quantum mirip dengan pemahaman pelajar catur yang lambat belajar. Kita sudah mengetahui aturannya selama lebih dari 70 tahun, dan kita membuat beberapa langkah cerdik yang bekerja dalam beberapa situasi khusus, tapi kita baru perlahan-lahan belajar prinsip-prinsip tingkat tinggi yang dibutuhkan untuk memainkan permainan yang cakap secara keseluruhan.
Overview
Informasi Quantum
- Informasi tidaklah murni matematis. Justru ia selalu memiliki wujud fisikal. Dalam ilmu informasi tradisional, wujud ini mengikuti fisika klasik, atau nonquantum. Perkembangan ilmu informasi quantum menaruh informasi dalam konteks quantum.
- Sumberdaya dasar informasi quantum adalah bit, yang berupa 0 atau 1. Informasi quantum terdiri dari bit-bit quantum, atau qubit (dilafalkan sebagai “cue-bit”). Qubit dapat eksis dalam superposisi, yang secara serempak melibatkan 0 dan 1, dan kelompok-kelompok qubit yang bisa “dijerat”, yang memberi mereka hubungan kontraintuitif.
- Komputer quantm yang memproses qubit, terutama qubit-qubit terjerat, bisa melampaui kinerja komputer klasik. Keterjeratan berperilaku seperti sumberdaya, mirip dengan energi, yang bisa dipakai untuk melakukan pemrosesan informasi quantum.
- Sasaran ilmu informasi quantum adalah memahami prinsip-prinsip umum tingkat tinggi yang mengatur sistem-sistem quantum kompleks semisal komputer quantum. Prinsip ini berhubungan dengan hukum mekanika quantum sebagaimana heuristik berhubungan dengan aturan dasar catur dalam permainan yang cakap.
Penemuan prinsip-prinsip ini merupakan sasaran ilmu informasi quantum, sebuah bidang fundamental yang sedang terbuka lebar sebagai jawaban terhadap cara baru memahami dunia. Banyak artikel ilmu informasi quantum fokus pada penerapan teknologi: kelompok-kelompok riset “menteleportasikan” status-status quantum dari satu lokasi ke lokasi lain. Fisikawan lain menggunakan status quantum untuk menciptakan kunci kriptografi yang aman sepenuhnya dari penyadapan. Para ilmuwan informasi memikirkan algoritma untuk komputer mekanis quantum hipotetis, jauh lebih cepat daripada algoritma untuk komputer konvensional atau klasik.
Teknologi-teknologi ini mengagumkan, tapi mengaburkan fakta bahwa mereka hanyalah produk sampingan penyelidikan tentang pertanyaan-pertanyaan ilmiah baru dan mendalam. Penerapan semisal teleportasi quantum memainkan peran yang mirip dengan mesin uap dan mesin lainnya yang memacu perkembangan termodinamika pada abad 18 dan 19. Termodinamika didorong oleh pertanyaan-pertanyaan dasar dan mendalam tentang bagaimana energi, panas, dan temperatur saling berkaitan, transformasi antara kuantitas-kuantitas ini dalam proses fisikal, dan peran kunci entropi.
Demikian halnya, ilmu informasi quantum mengukur hubungan antara satuan informasi klasik dan quantum, cara-cara baru agar informasi quantum bisa diproses, dan signifikansi penting sebuah fitur quantum yang disebut keterjeratan (entanglement), yang membawakan hubungan ganjil antara berbagai objek.
Keterangan populer seringkali menyajikan keterjeratan sebagai atribut wajib di mana partikel-partikel quantum [disebut] saling terjerat atau tidak sama sekali. Ilmu informasi quantum telah mengungkap bahwa keterjeratan adalah sumberdaya fisik yang bisa diukur, seperti energi, yang memungkinkan tugas-tugas pemrosesan energi: beberapa sistem memiliki sedikit keterjeratan; sedangkan sistem lainnya punya banyak. Semakin banyak keterjeratan yang ada, semakin cocok sebuah sistem dengan pemrosesan informasi quantum.
Lebih jauh, ilmuwan sudah mulai mengembangkan hukum kuantitatif keterjeratan yang hebat (analogis dengan hukum termodinamika yang mengatur energi), yang menyediakan seperangkat prinsip tingkat tinggi untuk memahami perilaku keterjeratan dan menggambarkan bagaimana kita dapat memakainya untuk melakukan pemrosesan informasi.
Ilmu informasi quantum masih cukup baru sehingga para periset masih berusaha memahami sifat dasarnya, dan belum sepakat tentang persoalan mana yang terdapat di pusatnya. Dari sudut pandang saya, sasaran pokok ilmu informasi quantum adalah mengembangkan prinsip-prinsip umum, seperti hukum keterjeratan, yang akan memungkinkan kita memahami kompleksitas pada sistem-sistem quantum.
Kompleksitas dan Quantum
Banyak studi kompleksitas berkonsentrasi pada sistem-sistem, misalnya cuaca atau tumpukan pasir, yang dideskripsikan oleh fisika klasik ketimbang fisika quantum. Fokus tersebut wajar sebab sistem kompleks biasanya makroskopis, mengandung banyak konstituen, dan kebanyakan sistem kehilangan sifat quantumnya begitu ukuran mereka ditingkatkan. Transisi quantum menuju klasik ini terjadi karena sistem quantum besar umumnya berinteraksi kuat dengan lingkungan mereka, menimbulkan proses dekoherensi, yang merusak atribut quantum sistem [lihat “100 Tahun Misteri Quantum”, tulisan Max Tegmark dan John A. Wheeler, Scientific American, Februari 2001].
Sebagai contoh dekoherensi, bayangkan kucing terkenal Erwin Schrödinger di dalam boks. Secara prinsip, kucing tersebut berakhir dalam status quantum yang ganjil, antara mati dan hidup; sulit menyatakannya mati atau hidup. Namun, dalam eksperimen riil, kucing berinteraksi dengan boks melalui pertukaran cahaya, panas, dan suara, dan boks pun berinteraksi dengan dunia. Dalam beberapa nanodetik, proses-proses ini merusak status-status quantum halus di dalam boks dan menggantinya dengan status-status yang bisa dideskripsikan oleh hukum fisika klasik hingga tingkat penaksiran yang bagus. Kucing di dalam betul-betul hidup atau mati, bukan dalam suatu status misterius nonklasik yang mengkombinasikan keduanya.
Kunci untuk melihat perilaku quantum pada sistem kompleks adalah mengisolasi sistem secara ekstrim dari dunia, mencegah dekoherensi, dan mempertahankan status quantum yang rapuh. Isolasi ini relatif mudah dilakukan pada sistem-sistem kecil, misalnya atom yang dijebak pada perangkap magnetik di ruang vakum, tapi jauh lebih sulit pada sistem besar di mana dijumpai perilaku kompleks. Penemuan-penemuan fenomena luar biasa semisal superkonduktivitas dan efek quantum Hall di laboratorium secara tak sengaja merupakan contoh di mana fisikawan telah mencapai sistem quantum besar yang terisolir. Fenomena-fenomena ini menunjukkan bahwa aturan sederhana mekanika quantum bisa melahirkan prinsip-prinsip berubah-ubah yang mengatur perilaku kompleks.
Sumberdaya dan Tugas
Kita berupaya memahami prinsip tingkat tinggi yang berlaku pada contoh-contoh langka tersebut ketika quantum dan kompleksitas bertemu, dengan mengabstraksi, mengadaptasi, dan memperluas alat-alat dari teori informasi klasik. Pada 2001, Benjamin W. Schumacher dari Kenyon College mengajukan bahwa unsur-unsur esensial ilmu informasi, baik klasik maupun quantum, bisa diringkas sebagai prosedur tiga langkah:
- Identifikasi sumberdaya fisik. Contoh klasik familiar adalah deretan bit. Walaupun bit sering dianggap sebagai entitas abstrak—0 dan 1—semua informasi tak pelak terenkode pada objek-objek fisik riil, jadi deretan bit mesti dianggap sebagai sumberdaya fisik.
- Identifikasi tugas pemrosesan informasi yang bisa dilakukan menggunakan sumberdaya fisik di langkah 1. Contoh klasik adalah tugas dua bagian berupa mengkompresi output dari sumber informasi (contohnya, teks pada buku) menjadi deretan bit lalu mendekompresinya—yakni, memulihkan informasi asli dari deretan bit yang dikompresi.
- Identifikasi kriteria keberhasilan penyelesaian tugas langkah 2. Dalam contoh kita, kriterianya adalah bahwa output dari tahap dekompresi cocok sempurna dengan input tahap kompresi.
Kalau begitu, pertanyaan fundamental ilmu informasi adalah “Berapa kuantitas minimal sumberdaya fisik (1) yang kita perlukan untuk melakukan tugas pemrosesan informasi (2) sesuai dengan kriteria keberhasilan (3)?” Walaupun tidak menangkap keseluruhan ilmu informasi, pertanyaan ini menyediakan lensa hebat untuk menatap banyak riset di bidang ini [lihat boks di bawah].
Contoh kompresi data bisa disamakan dengan pertanyaan dasar ilmu informasi klasik—yakni, berapa bilangan minimum bit yang dibutuhkan untuk menyimpan informasi yang dihasilkan oleh suatu sumber? Persoalan ini dipecahkan oleh Claude E. Shannon dalam paper–paper tahun 1948 yang terkenal yang mendirikan teori informasi. Dalam melakukannya, Shannon mengukur kandungan informasi yang dihasilkan oleh suatu sumber informasi, menetapkannya sebagai bilangan minimum bit yang dibutuhkan untuk menyimpan output sumber secara andal. Ekspresi matematis Shannon untuk kandungan informasi kini dikenal sebagai entropi Shannon.
Entropi Shannon muncul sebagai jawaban terhadap pertanyaan fundamental sederhana tentang pemrosesan informasi klasik. Maka tak mengejutkan bahwa mempelajari atribut-atribut entropi Shannon terbukti membuahkan hasil dalam menganalisa proses-proses yang jauh lebih kompleks daripada kompresi data. Contoh, ia memainkan peran sentral dalam mengkalkulasi berapa banyak informasi yang bisa ditransmisikan secara andal melalui kanal komunikasi berderau (ber-noise) dan bahkan dalam memahami fenomena seperti judi dan perilaku pasar saham. Tema umum ilmu informasi adalah bahwa pertanyaan mengenai proses-proses elementer membawa pada penyatuan konsep-konsep yang merangsang pemahaman tentang proses yang lebih kompleks.
Dalam ilmu informasi quantum, ketiga unsur pada daftar Schumacher memuat kekayaan baru. Apa sumberdaya fisik baru yang tersedia dalam mekanika quantum? Apa tugas pemrosesan informasi yang bisa kita lakukan? Apa kriteria keberhasilan yang sesuai? Sumberdaya fisik kini mencakup status-status superposisi, seperti kucing hidup dan mati. Proses-proses bisa melibatkan manipulasi keterjeratan (korelasi quantum misterius) antara objek-objek yang terpisah jauh. Kriteria keberhasilan jadi lebih halus daripada dalam fisika klasik, sebab untuk mengekstrak hasil tugas pemrosesan informasi quantum, kita harus mengamati, atau mengukur, sistem—yang tak pelak hampir mengubahnya, merusak status-status superposisi istimewa khas fisika quantum.
Qubit
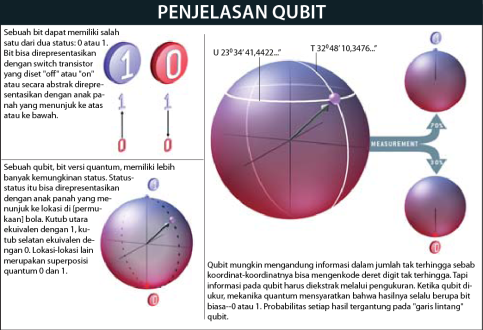
Ilmu informasi quantum dimulai dengan menggeneralisir sumberdaya fundamental informasi klasik—bit—menjadi bit quantum, atau qubit. Sebagaimana bit merupakan objek ideal yang diabstraksi dari prinsip-prinsip fisika klasik, qubit adalah objek quantum ideal yang diabstraksi dari prinsip-prinsip mekanika quantum. Bit bisa direpresentasikan dengan kawasan-magnetik pada cakram, voltase pada sirkuit, atau tanda grafit yang dibuat pensil pada kertas. Pemfungsian status-status fisikal klasik ini sebagai bit tidak bergantung pada detil bagaimana mereka direalisasikan. Demikian halnya, atribut-atribut qubit adalah independen dari representasi fisikal spesifik sebagai pusingan nukleus atom atau, katakanlah, polarisasi photon cahaya.
Bit digambarkan oleh statusnya, 0 atau 1. Begitu pula, qubit digambarkan oleh status quantumnya. Dua status quantum potensial untuk qubit ekuivalen dengan 0 dan 1 bit klasik. Namun dalam mekanika quantum, objek apapun yang memiliki dua status berbeda pasti memiliki rangkaian status potensial lain, disebut superposisi, yang menjerat kedua status hingga derajat bermacam-macam. Status-status qubit yang diperkenankan persisnya merupakan semua status yang harus bisa dicapai, secara prinsip, oleh bit klasik yang ditransplantasikan ke dalam dunia quantum. Status-status qubit ekuivalen dengan titik-titik di permukaan bola, di mana 0 dan 1 sebagai kutub selatan dan utara [lihat boks di bawah]. Kontinum status antara 0 dan 1 membantu perkembangan banyak atribut luar biasa informasi quantum.
Berapa banyak informasi klasik yang bisa kita simpan pada qubit? Sebuah garis pertimbangan menyebut besarannya tak terhingga: untuk merinci status quantum, kita perlu merinci garis lintang dan garis bujur titik ekuivalen pada bola, dan secara prinsip, masing-masing memiliki presisi sembarang. Bilangan-bilangan ini bisa mengenkode deretan bit panjang. Contoh, 011101101… bisa dienkode sebagai status bergaris lintang 01 derajat, 11 menit, 01,101… detik.
Pertimbangan ini, meski masuk akal, tidak tepat. Kita bisa mengkode besaran informasi klasik tak terhingga pada qubit tunggal, tapi kita takkan bisa memperoleh kembali informasi tersebut dari qubit. Upaya sederhana untuk membaca status qubit, patokan standar langsungnya, akan memberi hasil 0 atau 1, kutub selatan atau utara, di mana probabilitas tiap hasil ditentukan oleh garis lintang status asli. Anda bisa memilih patokan berbeda, barangkali menggunakan sumbu “Melbourne-Kepulauan Azores” ketimbang utara-selatan, tapi lagi-lagi hanya satu bit informasi yang bisa diekstrak, walau satu bit ini diatur oleh probabilitas berketergantungan berbeda pada garis lintang dan garis bujur status. Patokan manapun yang Anda pilih akan menghapus semua informasi pada qubit kecuali satu bit yang diungkap oleh patokan.
Prinsip-prinsip mekanika quantum mencegah kita mengekstrak lebih dari satu bit informasi, tak peduli seberapa cerdik kita mengenkode qubit atau seberapa cerdik kita mengukurnya sesudahnya. Hasil mengejutkan ini dibuktikan pada 1973 oleh Alexander S. Holevo dari Steklov Mathematical Institute di Moscow, menyusul penaksiran tahun 1964 oleh J.P. Gordon dari AT&T Bell Laboratories. Seolah, qubit mengandung informasi tersembunyi yang bisa kita manipulasi tapi tak bisa diakses secara langsung. Namun sudut pandang yang lebih baik adalah mengakui informasi tersembunyi ini sebagai satuan informasi quantum ketimbang bilangan bit klasik tak terhingga yang tak bisa diakses.
Perhatikan bagaimana contoh ini mengikuti paradigma Schumacher untuk ilmu informasi. Gordon dan Holevo bertanya berapa banyak qubit (sumberdaya fisik) yang diperlukan untuk menyimpan sejumlah tertentu informasi klasik (tugas) agar informasi tersebut bisa dipulihkan (kriteria keberhasilan). Selanjutnya, untuk menjawab pertanyaan ini, mereka memperkenalkan sebuah konsep matematika, kini dikenal sebagai Holevo chi (dilambangkan dengan huruf Yunani χ), yang sejak saat itu dipakai untuk menyederhanakan analisa fenomena yang lebih kompleks, serupa dengan penyederhanaan yang dimungkinkan oleh entropi Shannon. Contoh, Michael Horodecki dari Universitas Gdansk di Polandia telah menunjukkan bahwa Holevo chi bisa dipakai untuk menganalisa persoalan pengkompresian status-status quantum yang dihasilkan oleh sumber informasi quantum, yang analogis dengan kompresi data klasik yang dipertimbangkan oleh Shannon.
Status Terjerat
Qubit-qubit tunggal memang menarik, tapi perilaku yang lebih mengagumkan timbul ketika beberapa qubit disatukan. Fitur kunci ilmu informasi quantum adalah pemahaman bahwa kelompok-kelompok yang terdiri dari dua objek quantum atau lebih bisa memiliki status-status yang terjerat. Status-status terjerat ini mempunyai atribut yang secara fundamental berbeda dari [status dalam] fisika klasik dan dianggap sebagai tipe sumberdaya fisik baru yang dapat dipakai untuk melakukan tugas-tugas menarik.
Sistem-sistem quantum terjerat berperilaku dengan cara yang di dunia klasik mustahil terjadi.
Schrödinger begitu terkesan oleh keterjeratan sehingga dalam sebuah paper seminal tahun 1935 (tahun yang sama ketika dia memperkenalkan kucingnya kepada dunia) dia menyebutnya “memang ciri khas mekanika quantum, menyimpang sepenuhnya dari garis-garis pemikiran klasik.” Anggota-anggota sekumpulan objek terjerat tidak mempunyai status quantum tersendiri. Hanya kelompok tersebut secara keseluruhan yang memiliki status jelas [lihat boks di bawah]. Fenomena ini jauh lebih ganjil daripada status superposisi sebuah partikel. Partikel semacam itu memiliki status quantum jelas meskipun status tersebut mungkin bersuperposisi status-status klasik berlainan.
Objek-objek terjerat berperilaku seolah mereka terhubung dengan satu sama lain, tak peduli seberapa jauh mereka terpisah—jarak tidak melemahkan keterjeratan sedikitpun. Jika sesuatu terjerat dengan objek lain, pengukurannya serta-merta menyediakan informasi mengenai partnernya. Mudah sekali tersesat ke dalam pemikiran bahwa kita bisa memanfaatkan keterjeratan untuk mengirim sinyal lebih cepat daripada cahaya, melanggar relativitas khusus Einstein, tapi sifat probabilistik mekanika quantum menghalangi upaya semacam itu.
Terlepas dari keanehannya, untuk waktu lama keterjeratan dianggap sebagai barang aneh dan sebagian besar diabaikan oleh fisikawan. Ini berubah pada 1960-an, ketika John S. Bell dari CERN, laboratorium fisika partikel Eropa dekat Jenewa, memprediksi bahwa status-status quantum terjerat memperkenankan pengujian eksperimen krusial yang membedakan mekanika quantum dan fisika klasik. Bell memprediksi, dan para pelaku eksperimen telah mengkonfirmasi, bahwa status-status quantum terjerat memperagakan perilaku yang mustahil di dunia klasik—perilaku ini mustahil, sekalipun kita bisa mengubah hukum fisika untuk mencoba mengemulasi prediksi quantum dalam kerangka klasik apapun! Keterjeratan merepresentasikan fitur baru dunia kita yang sulit dipikirkan oleh para pakar sekalipun. Walaupun kita bisa menggunakan matematika teori quantum untuk menalar keterjeratan, segera setelah kita mencari jalan dengan analogi-analogi, terdapat bahaya besar bahwa landasan klasik analogi kita akan menyesatkan.
Pada awal 1990-an, ide bahwa keterjeratan sepenuhnya berada di luar lingkup fisika klasik mendorong periset bertanya-tanya apakah keterjeratan bisa berguna sebagai sumberdaya untuk memecahkan persoalan pemrosesan informasi dengan cara-cara baru. Jawabannya ya. Banjir contoh dimulai pada 1991, saat Artur K. Ekert dari Universitas Cambridge menunjukkan cara menggunakan keterjeratan untuk mendistribusikan kunci kriptografi yang tahan penyadapan. Pada 1992, Charles H. Bennett dari IBM dan Staphen Wiesner dari Universitas Tel Aviv menunjukkan bahwa keterjeratan dapat membantu mengirim informasi klasik dari satu lokasi ke lokasi lain (sebuah proses yang disebut pengkodean super-rapat, di mana dua bit ditransfer dalam sebuah partikel yang memiliki ruang untuk mengangkut satu saja). Pada 1993, sebuah tim internasional yang terdiri dari enam orang menjelaskan cara menteleportasikan status quantum dari satu lokasi ke lokasi lain menggunakan keterjeratan. Ledakan penerapan lanjutan kemudian terjadi.
Menimbang Keterjeratan
Sebagaimana pada qubit-qubit individual, yang bisa direpresentasikan dengan banyak objek fisikal berlainan, keterjeratan juga memiliki atribut yang independen dari representasi fisikalnya. Secara praktik, mungkin lebih nyaman bekerja dengan satu sistem atau lebih, tapi secara prinsip tidak berpengaruh. Contoh, kita bisa melakukan kriptografi quantum dengan sepasang photon terjerat atau sepasang nukleus atom terjerat atau bahkan photon dan nukleus yang terjerat.
Ketergantungan representasi mengindikasikan analogi yang menggusarkan antara keterjeratan dan energi. Energi mematuhi hukum termodinamika, tak peduli entah itu energi kimiawi, energi nuklir, atau bentuk lainnya. Bisakah teori keterjeratan umum dikembangkan selaras dengan hukum termodinamika?
Harapan ini sangat didorong pada 1990-an, ketika periset menunjukkan bahwa berbagai bentuk keterjeratan adalah ekuivalen secara kualitatif—keterjeratan sebuah status bisa ditransfer ke status lain, serupa dengan energi yang mengalir dari, katakanlah, charger baterai ke baterai. Mengandalkan hubungan kualitatif ini, para peneliti mulai memperkenalkan ukuran kualitatif keterjeratan. Perkembangan ini sedang berlangsung, dan periset belum sepakat tentang cara terbaik mengukur keterjeratan. Skema paling sukses sejauh ini didasarkan pada gagasan satuan standar keterjeratan, mirip dengan satuan standar massa atau energi [lihat boks Mengurai Keterjeratan].
Pendekatan ini bekerja secara analogis pada pengukuran massa menggunakan kesetimbangan. Massa sebuah objek ditentukan oleh berapa banyak salinan massa standar yang diperlukan untuk menyetimbangkannya pada sederet skala. Para ilmuwan informasi quantum telah mengembangkan “kesetimbangan keterjeratan” teoritis untuk membandingkan keterjeratan dalam dua status berbeda. Besaran keterjeratan dalam sebuah status ditentukan dengan memperhatikan berapa banyak salinan suatu satuan standar tetap keterjeratan yang diperlukan untuk menyetimbangkannya. Perhatikan, metode pengukuran keterjeratan ini merupakan contoh lain pertanyaan fundamental dalam ilmu informasi. Kita telah mengidentifikasi sumberdaya fisik (salinan status terjerat kita) dan tugas dengan kriteria keberhasilan. Kita menetapkan ukuran keterjeratan kita dengan bertanya berapa banyak sumberdaya fisik yang kita butuhkan untuk melaksanakan tugas dengan sukses.
Ukuran kuantitatif keterjeratan yang dikembangkan dengan mengikuti program ini terbukti amat bermanfaat sebagai konsep penyatu dalam deskripsi banyak fenomena. Ukuran keterjeratan memperbaiki cara periset menganalisa tugas-tugas semisal teleportasi quantum dan algoritma komputer mekanis quantum. Analogi energi kembali membantu: untuk memahami proses-proses semisal reaksi kimiawi atau operasi mesin, kita mempelajari aliran energi antara bagian-bagian sistem dan menetapkan bagaimana energi harus dibatasi di berbagai lokasi dan waktu. Dengan cara serupa, kita bisa menganalisa aliran keterjeratan dari satu subsistem ke subsistem lain yang dibutuhkan untuk melakukan tugas pemrosesan informasi quantum sehingga memperoleh batasan sumberdaya yang diperlukan untuk melakukan tugas tersebut.
Perkembangan teori keterjeratan merupakan contoh pendekatan bottom-up—berawal dari pertanyaan sederhana mengenai penyetimbangan keterjeratan, kita lambat-laun mendapat pemahaman mengenai fenomena yang lebih kompleks. Kontrasnya, dalam beberapa kasus, orang-orang meramalkan fenomena amat kompleks lewat lompatan besar pemahaman, memungkinkan ilmu informasi quantum berkembang secara top-down. Contoh paling terkenal adalah algoritma untuk secara cepat menemukan faktor prima bilangan bulat campuran pada komputer quantum, dirumuskan tahun 1994 oleh Peter W. Shor dari AT&T Bell Labs. Pada komputer klasik, algoritma terbaik memakan lebih banyak sumberdaya untuk memfaktorkan bilangan-bilangan besar. Bilangan 500 digit memerlukan 100 juta kali langkah komputasi lebih banyak daripada bilangan 250 digit. Namun, biaya algoritma Shor naik secara polinomial saja—bilangan 500 digit hanya memerlukan delapan kali langkah lebih banyak daripada bilangan 250 digit.
Algoritma Shor adalah contoh lanjutan paradigma dasar (berapa banyak waktu komputasi diperlukan untuk menemukan faktor bilangan bulat n-bit?), tapi algoritma ini tampak terisolir dari kebanyakan temuan lain ilmu informasi quantum [lihat boks di bawah]. Sekilas, itu cuma seperti trik pemrograman cerdik dengan signifikansi fundamental yang kecil. Penampilan tersebut menipu; para periset telah menunjukkan bahwa algoritma Shor bisa ditafsirkan sebagai contoh prosedur untuk menetapkan level energi sistem quantum, sebuah proses yang fundamental. Seiring waktu berjalan dan kita mengisi lebih banyak pada peta, semestinya kian mudah memahami prinsip-prinsip yang mendasari algortima Shor dan algoritma quantum lainnya dan, kita harap, mengembangkan algoritma baru.
Satu penerapan terakhir, yakni koreksi error quantum, menyediakan bukti terbaik hingga kini bahwa ilmu informasi quantum merupakan kerangka bermanfaat untuk mempelajari dunia. Status quantum [bersifat] halus, mudah dirusak oleh interaksi yang bocor, atau derau (noise), sehingga skema untuk mengatasi disturbansi ini amat esensial.
Komputasi dan komunikasi klasik memiliki bermacam-macam kode pengkoreksi error yang dibangun dengan baik untuk melindungi informasi dari pengrusakan oleh derau. Contoh sederhana adalah kode repetisi [lihat boks di bawah]. Skema ini merepresentasikan bit 0 sebagai deret tiga bit, 000, dan bit 1 sebagai deret tiga bit, 111. Jika derau relatif lemah, terkadang dapat membalik salah satu bit pada triplet, mengubah, misalnya, 000 menjadi 010, tapi akan jarang membalik dua bit pada triplet. Kapanpun kita menjumpai 010 (atau 100 atau 001), kita bisa hampir yakin bahwa nilai yang tepat adalah 000, atau 0. Generalisasi ide ini secara lebih kompleks akan menyediakan kode pengkoreksi error yang amat bagus untuk melindungi informasi klasik.
Koreksi Error Quantum
Awalnya terasa mustahil mengembangkan kode untuk koreksi error quantum sebab mekanika quantum melarang kita mengetahui pasti status tak dikenal sebuah objek quantum—lagi-lagi, rintangan dalam mencoba mengekstrak lebih dari satu bit dari qubit. Oleh karena itu kode triplet klasik sederhana gagal, sebab kita tak bisa memeriksa tiap salinan qubit dan memeriksa bahwa satu salinan harus dibuang tanpa mengganggu semua salinan lain dalam proses tersebut. Yang lebih buruk lagi, membuat salinan bukanlah soal sepele: mekanika quantum melarang mengambil qubit tak dikenal dan membuat duplikat, sebuah temuan yang dikenal sebagai no-cloning theorem (teorema pelarang kloning).
Situasi tampak suram pada pertengahan 1990-an, ketika fisikawan-fisikawan terkemuka seperti alhamrhum Rolf Landauer dari IBM menulis artikel-artikel skeptis yang menguraikan bahwa koreksi error quantum akan dibutuhkan untuk komputasi quantum tapi teknik-teknik klasik standar tidak bisa dipakai dalam dunia quantum. Bidang ini berutang besar pada skeptisisme Landauer yang menguraikan masalah yang harus diatasi ini [lihat “Riding the Back of Electrons”, tulisan Gary Stix, Scientific American, September 1998].
Untunglah, ide-ide cerdik yang dikembangkan secara independen oleh Shor dan Andrew M. Steane dari Universitas Oxford pada 1995 menunjukkan bagaimana melakukan koreksi error quantum tanpa harus mengetahui status-status qubit atau mengkloningnya. Sebagaimana pada kode triplet, setiap nilai direpresentasikan dengan sederet qubit. Qubit-qubit ini diperjalankan melewati sirkuit (analogi quantum untuk gerbang logika) yang akan berhasil memperbaiki error pada qubit manapun tanpa sungguh-sungguh “membaca” bagaimana status-status individualnya. Seolah kita memasang triplet 010 menembus sirkuit yang bisa melihat bahwa bit tengah berbeda lalu membaliknya, tanpa menetapkan identitas ketiga bit itu.
Kode-kode pengkoreksi error quantum merupakan kemenangan sains. Sesuatu yang menurut orang-orang brilian tak bisa dilakukan—melindungi status-status quantum dari efek derau—dikerjakan menggunakan kombinasi konsep-konsep dari ilmu informasi dan mekanika quantum dasar. Teknik ini kini telah mendapat konfirmasi awal dalam eksperimen-eksperimen di Los Alamos National Laboratory, IBM, dan Massachusetts Institute of Technology, dan eksperimen yang lebih luas sudah direncanakan.
Koreksi error quantum juga telah merangsang banyak ide baru yang menggairahkan. Contoh, jam-jam terbaik dunia sekarang ini dibatasi oleh derau mekanis quantum; periset sedang bertanya-tanya apakah presisi jam-jam ini bisa diperbaiki dengan menggunakan koreksi error quantum. Ide lain, diusulkan oleh Alexei Kitaev dari California Institute of Technology, adalah bahwa beberapa sistem fisikal mungkin memiliki tipe toleransi derau alami. Sistem-sistem itu praktisnya akan menggunakan koreksi error quantum tanpa intervensi manusia dan mungkin memperlihatkan daya tahan luar biasa terhadap dekoherensi.
Kita sudah menggali bagaimana ilmu informasi quantum berkembang dari pertanyaan-pertanyaan fundamental untuk membangun pemahaman tentang sistem yang lebih kompleks. Bagaimana di masa depan? Dengan mengikuti program Schumacher, kita pasti akan memperoleh pemahaman baru mengenai kapabilitas alam semesta dalam memproses informasi. Barangkali metode-metode ilmu informasi quantum bahkan akan menghasilkan pemahaman tentang sistem-sistem yang secara tradisional tak dianggap sebagai sistem pemroses informasi. Contoh, materi terkondensasi memperagakan fenomena kompleks seperti superkonduktivitas yang bertemperatur tinggi dan efek quantum Hall yang kecil. Atribut-atribut quantum seperti keterjeratan ikut terlibat, tapi peran mereka saat ini belum jelas. Dengan menerapkan apa yang sudah kita ketahui dari ilmu informasi quantum, kita dapat meningkatkan keterampilan kita dalam pertandingan catur yang tengah berlangsung, melawan alam semesta quantum yang kompleks.
Penulis
Michael A. Nielsen merupakan associate professor di fakultas fisika Universitas Queensland di Brisbane, Australia. Lahir di Brisbane, dia menerima Ph.D.-nya dalam bidang fisika sebagai Fulbright Scholar di Universitas New Mexico pada 1998. Dia adalah penulis, bersama Isaac L. Chuang dari Massachusetts Institute of Technology, buku teks komprehensif pertama tingkat sarjana mengenai ilmu informasi quantum, Quantum Computation and Quantum Information.
Untuk Digali Lebih Jauh
- Quantum Theory and Measurement. Disunting oleh John A. Wheeler dan Wojciech H. Zurek. Memuat cetak-ulang paper–paper penting, termasuk terjemahan paper “paradoks kucing” karya Erwin Schrödinger tahun 193. Princeton University Press, 1983.
- The Fabric of Reality. David Deutsch. Penguin Books, 1998.
- The Bit and the Pendulum. Tom Siegfried. John Wiley & Sons, 2000.
- Quantum Computation and Quantum Information. Michael A. Nielsen dan Isaac L. Chuang. Cambridge University Press, 2000.
- Website Center for Quantum Computation: www.qubit.org.
- Catatan kuliah John Preskill tersedia di www.theory.caltech.edu/people/preskill/ph229/.
- Lihat www.sciam.com untuk artikel-artikel Scientific American yang terkait dengan ilmu informasi quantum.






6 thoughts on “Aturan Sederhana Untuk Dunia Quantum yang Kompleks”